Question 1
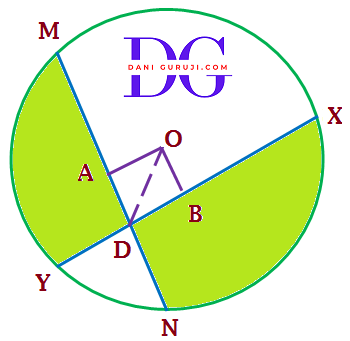
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm.
Find the length of the common chord.
Solution :
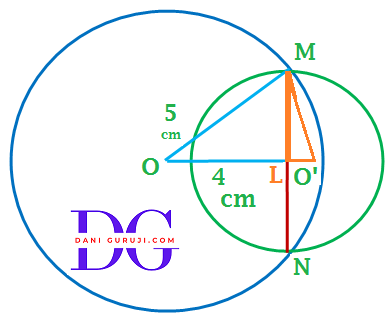
Let the radius of the circle centered at O and O' be 5 cm and 3 cm respectively,
and the distance between the centers of two circles is 4 Cm.
Given that the circles intersect at 2 points, M and N
Let MN be the common chord.
∴ OM = 5 Cm. and O'M = 3 Cm.
It can be observed that the radius of the bigger circle is more than the distance between the 2 centres,
we can say that the centre of smaller circle lies inside the bigger circle itself.
In two intersecting circles, The line segment connecting the centers of the two circles (OO') is the perpendicular bisector of the common chord MN.
∴ ML = LN and $\angle $ OLM = $\angle $ O'LM = 90°
Given that OO' = 4 Cm.
Consider that OL = x, so O'L = (4 - x)
Now, In the right-angled ∆ OLM ( using the larger circle's radius), we have
By using Pythagoras theorem
OM2 = ML2 + OL2
⇒ 52 = ML2 + x2
⇒ ML2 = 25 - x2 ....(i)
Now, In the right-angled ∆ O'LM ( using the smaller circle's radius), we have
By using Pythagoras theorem
O'M2 = ML2 + O'L2
⇒ 32 = ML2 + (4-x)2
⇒ ML2 = 9 - (4-x)2
⇒ ML2 = 9 - 16 + x2 − 8x
⇒ ML2 = - 7 - x2 + 8x .....(ii)
From equation (i) and (ii)
25 - x2 = - 7 - x2 + 8x
⇒ 8x = 32
⇒ x = 4
Hence, O'L = 4 - 4 = 0 cm ,
L and O′ coincide .
Thus, the common chord will pass through the center of the smaller circle
∴ MN is a diameter of the smaller circle.
⇒ ML = O'M = 3 cm
( Radius of smaller circle )
⇒ Length of the common chord MN = 2 × ML
⇒ (2 × 3) cm
⇒ MN = 6 Cm.
Thus, the required length of the common chord = 6 Cm .